MRI 噪声和去噪方法

1. 磁共振中的噪声

磁共振成像中的主要噪声源是热噪声，它来自被扫描对象以及接收器中的电子元件。

噪声通常根据扫描仪线圈结构进行统计建模。对于单线圈采集，复数的空间磁共振数据通常被建模为一个复数的高斯过程，其中原始信号的实部和虚部被均值为零、方差为 $σ_n^2$ 的不相关高斯噪声所破坏。因此，幅值信号就是复信号的 Rician 分布包络。

在考虑多线圈磁共振采集系统时，每个接收线圈都要重复高斯过程。因此，k 空间中每个线圈的噪声也可以建模为一个平均值为零，方差相等的复数静态加性白高斯噪声过程，在这种情况下，每个线圈的图像空间复合信号中的噪声也将是高斯噪声。如果对 k 空间进行了完全采样，则可使用诸如平方和（SoS）等方法获得复合幅度信号（CMS，即重建后的最终真实信号）。假定噪声分量是相同且独立分布的，CMS 将遵循非中心秩（nc-χ）分布。如果考虑到线圈之间的相关性，数据并不严格遵循 nc-χ 分布，但出于实用目的，可以将其建模为 nc-χ 分布，但要考虑到有效参数。

然而，在多线圈系统中，对 k 空间进行完全采样采集并不是采集的普遍趋势。如今，由于时间限制，大多数采集通常通过使用并行 MRI（pMRI）重建技术来加速，通过对 k 空间进行欠采样采集来提高采集率。这种加速与一种被称为 “混叠”（aliasing）的伪像同时出现。

为了抑制欠采样产生的混叠，人们提出了许多重建方法，其中以 SENSE（快速磁共振成像灵敏度编码） 和 GRAPPA（广义自动校准部分并行采集）为主。从统计学角度来看，这两种重建方法都会影响重建数据中噪声的静态性，即噪声在整个图像中的空间分布。因此，如果使用 SENSE，幅值信号可被视为 Rician 分布，但统计参数值，尤其是噪声方差 σn2 会因图像位置不同而不同，即与 x 有关。同样，如果使用 GRAPPA，则 CMS 可近似为具有有效参数的非稳态 nc-χ 分布。[1]

并行成像技术的使用引入了随空间变化的非均匀高斯噪声分布。

通过将原始信号空间中的空间无关噪声分布传入到图像重建流水线的所有步骤中，可以得到一个噪声图，该噪声图指定了最终图像中每个像素的噪声标准偏差。在噪声调整扫描的基础上，确定热噪声水平和去相关矩阵。在实际的图像重建中，可以从带有单变量高斯噪声的去相关 k 空间数据中检索动这些信息，通过顺序重建步骤的传播确定噪声图，从而得到具有高斯噪声分布和每个像素已知标准偏差的复值图像。整个过程如图 1 所示。

图1. 空间不变的热噪声分布通过图像重建流水线传播，形成空间变异的高斯分布[2]。

首先，作为扫描仪调整的一部分，通过在没有射频激励的情况下，进行的快速噪声校准扫描，确定源于热噪声分布的每个 k 空间样本的标准偏差。其次，考虑重建过程导致的噪声分布变化，包括 k 空间滤波和傅立叶变换缩放。随空间变化的噪声强度受线圈几何因子（称为 g 因子）的影响。对于广义自动校准部分并行采集（GRAPPA） 而言，这一 g 因子可以直接从 GRAPPA 重建权重和通道组合系数中推导出来。要确定重建图像的噪声分布，需要将原始标准偏差与 GRAPPA 重建的噪声增强值相乘。接下来的步骤是表面线圈强度校正。放置在患者周围的表面线圈在靠近身体表面的地方灵敏度较高，而来自身体内部较远区域的信号则会出现衰减。将图像与相应的偏置场相乘可校正由此产生的强度变化，偏置场可在测量前通过单独扫描进行估算。

因此，空间分辨的噪声图是初始标准偏差、g 因子和偏置场的乘法组合。需要注意的是，噪声去相关步骤被纳入处理流程，并在重建之前执行，这样噪声相关矩阵 Σ 变成对角矩阵。[2]

2. 磁共振图像去噪

降噪技术有两个主要方向：

• 基于采集的信号增强和，
• 在重建过程中或重建后进行降噪。

在图像采集过程中，可以通过重复测量的平均值来提高信噪比，从而延长采集时间，或者通过扩大体素尺寸来增加信号强度。然而，在实际操作中，由于扫描仪的吞吐量和病人舒适度等各种因素，图像采集时间受到限制。使用更大的体素又进一步限制了空间分辨率。因此，对于大多数磁共振成像应用来说，信噪比都有一个实际上限。

在重建过程中使用特定算法对获取的图像进行去噪，例如通过感知压缩、在重建后对图像进行滤波、或两者相结合，都是低成本、高效率的替代方法。

2.1 传统算法

传统的磁共振成像去噪技术一般基于滤波、变换或统计方法，如 Mohan 等人（2014 年）的研究。目前使用最广泛的三种方法是 Tomasi 和 Manduchi（1998 年）的双边滤波、Buades 等人（2005 年）的 non-local means 和 Dabov 等人（2007 年）的 BM3D。

Tomasi 和 Manduchi（1998 年）提出的双边滤波器是一种保留边缘的非迭代方法。当应用于图像时，它使用一个低通去噪的核，根据原始图像的像素值的空间分布进行调整。这有助于在去噪的同时保留图像边缘。在存在尖锐过渡的情况下，核会根据这种过渡进行加权，由图像的强度值和非线性加权函数的卷积建模的。

import cv2
def bilaterFilter(image):
    maxv = np.max(image)
    image = image / maxv * 255
    image = image.astype(np.uint8)
    # 应用双边滤波
    # 参数说明：
    # d: 滤波时周围每个像素邻域的直径
    # sigmaColor: 颜色空间过滤器的 sigma 值，大的 sigma 值意味着颜色越远的像素会混合在一起
    # sigmaSpace: 坐标空间中滤波器的 sigma 值，大的值意味着只有颜色足够接近的像素才会影响彼此
    filtered_image = cv2.bilateralFilter(image, d=2, sigmaColor=5, sigmaSpace=75)
    filtered_image = filtered_image / 255 * maxv
    return filtered_image

Buades 等人（2005 年）提出的non-local mean（NLM）利用了自然图像所具有的自空间相似性。它利用邻近像素的冗余来去除噪声。这种滤波器的简单之处在于，利用这些相似性，在图像的其他部分找到与正在去噪的 patch 相似的 patch。这就是所谓的邻域滤波。NLM 根据与原始 patch 的相似度及其与观察 patch 中心的距离来分配置信度权重。NLM 的主要问题在于，由于它依赖于大空间搜索，因此会在计算方面造成瓶颈。下面代码里的 cv2.fastNlMeansDenoising 应该是经过优化的，实测比 BM3D快一些。

def non_local_mean(image):
    maxv = np.max(image)
    image = image / maxv * 255
    image = image.astype(np.uint8)
    # 应用非局部均值去噪
    
    denoised_image = cv2.fastNlMeansDenoising(image, h=1)
    denoised_image = denoised_image / 255 * maxv
    return denoised_image

Dabov 等人（2007 年）提出的 BM3D 是 NLM 的扩展，因为它使用了图像中的空间相似性。它首先要搜索的是与正在去噪的 patch 具有相似强度的 patch 。建立一个包含 patch 大小和聚集 patch 的三维矩阵。然后，应用 3D 变换。为了去除高频噪声，对变换空间进行过滤和阈值处理。最后，通过反变换得到去噪三维块。为了恢复原始阵列，需要为每个 patch 分配基于 patch 的方差和距离权重。

# pip install bm3d
imoprt bm3d
def BM3D(image):
    sigma = 2.5
    # Apply BM3D denoising
    denoised_image = bm3d.bm3d(image, sigma)
    return denoised_image

2.2 Supervised learning

有监督的深度学习方法需要成对的有噪声和无噪声图像进行训练。

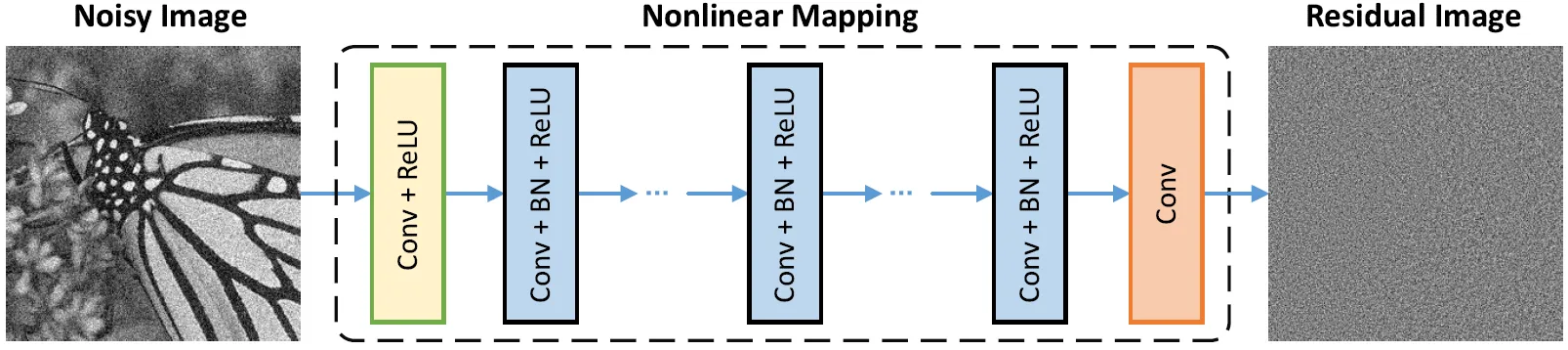
一种最著名的监督去噪方法是 DnCNN，使用前馈卷积神经网络（CNN），使用了残差模块和BatchNorm，预测噪声图像和潜在干净图像之间的残差图像。此外，它不需要知道噪声的水平，可以执行盲高斯去噪。[4]

图2. DnCNN

FFDNet 通过输入可调节的噪声水平图，在下采样的子图像上进行去噪，实现了速度与性能的平衡。能够通过单一网络处理广泛的噪声水平，去除空间变化噪声。作者将噪声水平 sigma 设置为一个大小与输入相同的patch，实现噪声水平的输入。[5] 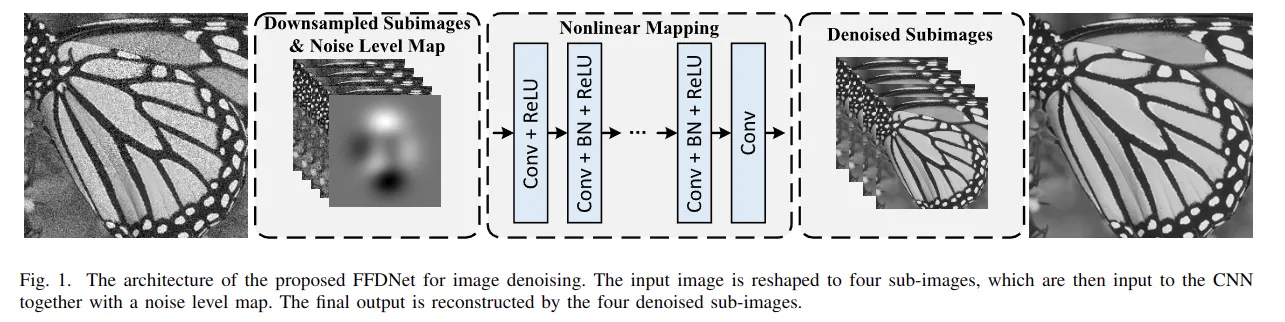图3. FFDNet

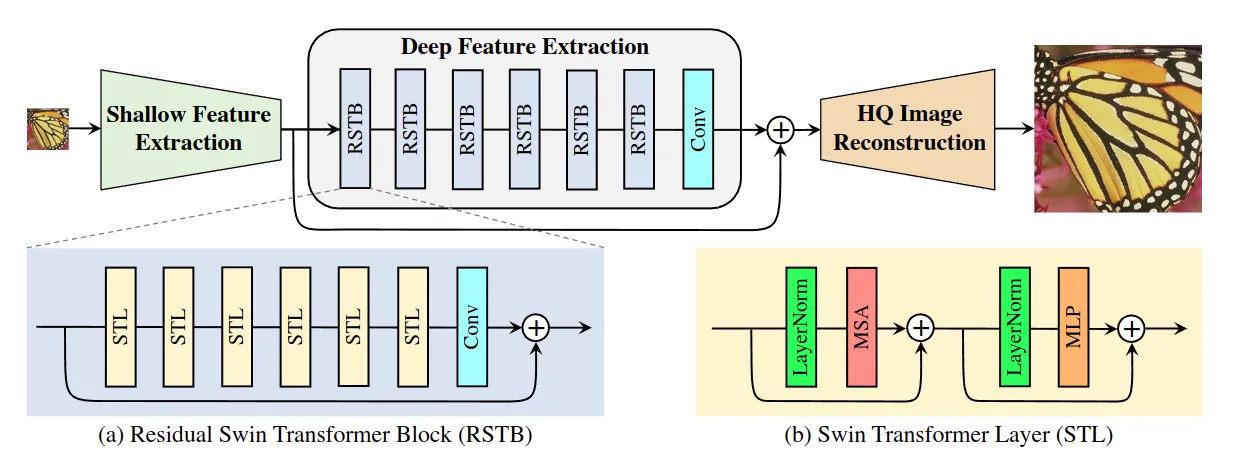
SwinIR 使用 Swin Transformer 进行图像去噪任务。它将 Transformer 与 CNN 结合，利用 Transformer 的长距离依赖捕捉能力和 CNN 的特征融合能力，有效提升了去噪效果。

图4. SwinIR

以上模型的代码：Training and testing codes for USRNet, DnCNN, FFDNet, SRMD, DPSR, MSRResNet, ESRGAN, BSRGAN, SwinIR, VRT, RVRT

针对于 MRI 图像的去噪

Jiang 等人（2018 年）提出了使用多通道 DnCNN 对磁共振成像中的 Rician 噪声而不是高斯噪声进行去噪。[6]

Duo 等人提出了一种用于MRI去噪的复值卷积神经网络（非盲DnCNN），旨在解决传统去噪方法忽视相位信息的问题。该网络通过引入噪声水平图，能够有效处理模拟和真实低场MRI数据中的噪声。网络的输入是一个 2D 复值 MRI 图像，与可调节的复值噪声级别图拼接在一起。非盲ℂDnCNN 由一系列复数卷积块组成。每个块中采用了三种操作：复数卷积（ℂConv）、径向批量标准化（BN）和复数修正线性单元（ℂReLU）。噪声等级由分别估计实部和虚部的 sigma 平均得到。[7]

2.3 Unspervised learning

然而，在核磁共振成像中，获取严格无噪声的图像并不可行。在这种情况下，可以采用无监督学习方法，从而避免在模型训练过程中需要成对的干净图像。

用于无监督去噪的最有效模型之一是 Soltanayev 和 Chun（2018 年）提出的基于 Stein 的无偏风险估计器 SURE。SURE 估计器是一种无偏 MSE 估计器，，其优势在于能够以解析形式表示，从而直接用于某些去噪任务。然而，当无法直接使用解析形式时，例如在复杂模型中，需要借助近似方法。Ramani 等人（2008 年）提出了一种基于蒙特卡洛的 SURE，即 MC-SURE。Soltanayev 和 Chun（2018）提出的工作克服了之前的不足，结合了蒙特卡洛近似，并使其适用于深度神经网络模型。采用斯坦因无偏风险估计器（SURE）作为损失函数，通过将高斯噪声分布的方差纳入各种计算机视觉应用中，来近似计算输出图像与未知 groundtruth之间的均方误差（MSE）。

Noise2Noise 通过使用两个独立的噪声图像上进行训练，学会从另一幅图像中预测一幅噪声图像，预测每个像素的噪声分布期望值的模型。对于高斯、泊松等许多真实噪声模型来说，这个期望值就是干净的信号。然而，这种方法需要成对的噪声图像，限制了其应用范围。

而 Noise2Void 则采用盲点技术来预测被遮挡的图像块，不再需要两个独立样本，通过训练，网络可利用周围未屏蔽的像素预测屏蔽像素值。 Noise2Self 引入 J 不变性，避免了显式遮蔽像素，提高了效率。

Noisier2Noise 建立在 Noise2Noise、Noise2Void 和 Noise2Self 的方法之上。该方法只需要每个训练样例的单个噪声实现和噪声分布的统计模型，适用于各种噪声模型，包括空间结构化噪声。它从统计模型中生成一个合成噪声样本，将其添加到已经有噪声的图像中，并要求网络从这个双噪声图像中预测原始噪声图像，从而实现去噪。

Neighbor2Neighbor 是 Noise2Noise 的扩展，通过理论分析将 Noise2Noise 推广到了单张含噪图像和相似含噪图像这两个场景，并通过设计采样器的方式从单张含噪图像构造出相似含噪图像，通过引入正则项的方式解决了采样过程中相似含噪图像采样位置不同而导致的图像过于平滑的问题。

方法	训练数据	核心思想	优势	局限性
Noise2Noise	成对的噪声图像	使用成对的噪声输入进行训练	性能高	需要成对的噪声图像
Noise2Void	单个噪声图像	遮蔽像素，从周围区域进行预测	不需要成对数据	受限于遮蔽策略
Noise2Self	单个噪声图像	J-不变性，自监督	比Noise2Void有改进	减少了可用像素信息
Noisier2Noise	单个噪声图像	在训练中添加合成噪声	可以处理未配对的噪声数据	需要额外的噪声假设
Neighbor2Neighbor	单个噪声图像	使用随机子图像进行训练	不需要遮蔽或成对数据	受限于随机子图像分割

Noise2score 通过确定后验分布的模式来解决图像去噪问题，通过与 Tweedie 公式相结合对任何指数族噪声进行图像去噪。

针对于 MRI 图像的去噪

Noise2Contrast，是一种自监督技术，利用各种测量的 MR 图像对比度信息来训练去噪模型。其他方法则考虑整合额外的先验信息，以获得更接近监督训练的结果。

DDM2（Denoising Diffusion Models for Denoising Diffusion MRI），利用扩散去噪生成模型进行MRI去噪的自监督去噪方法。提出的三阶段框架将基于统计的去噪理论整合到扩散模型中，并通过条件生成进行去噪。

Chung 等人（2022）提出了一种基于分数反向扩散采样的去噪方法，仅使用膝关节冠状扫描进行训练，即使在受到复杂混合噪声污染的分布外体内肝脏 MRI 数据上也表现出色。此外，还提出了一种用同一网络提高去噪图像分辨率的方法。[8]

参考论文

[1] Noise estimation in parallel MRI: GRAPPA and SENSE

[2] Self-supervised MRI denoising: leveraging Stein’s unbiased risk estimator and spatially resolved noise maps.

[3] Evaluation of MRI Denoising Methods Using Unsupervised Learning.

[4] Zhang, K., Zuo, W., Chen, Y., Meng, D., and Zhang, L. (2017). Beyond a Gaussian Denoiser: Residual Learning of Deep Cnn for Image Denoising. IEEE Trans. Image Process. 26, 3142–3155. doi:10.1109/TIP.2017.2662206Accessed November 28, 2020

[5] Zhang, K., Zuo, W., & Zhang, L. (2018). FFDNet: Toward a fast and flexible solution for CNN-based image denoising. IEEE Transactions on Image Processing, 27(9), 4608-4622.

[6] Jiang, D., Dou, W., Vosters, L., Xu, X., Sun, Y., and Tan, T. (2018). Denoising of 3D Magnetic Resonance Images with Multi-Channel Residual Learning of Convolutional Neural Network. Jpn. J. Radiol. 36, 566–574. doi:10.1007/s11604-018-0758-8Accessed November 28, 2020

[7] Dou, Q., Wang, Z., Feng, X., Campbell‐Washburn, A. E., Mugler III, J. P., & Meyer, C. H. (2025). MRI denoising with a non‐blind deep complex‐valued convolutional neural network. NMR in Biomedicine, 38(1), e5291

[8] MR Image Denoising and Super-Resolution Using Regularized Reverse Diffusion.