文章

MRI 成像（二）：K空间与快速成像

发表于
作者 big fish is watching you 23 分钟阅读

空间定位

在均匀的主磁场中，MR接收线圈所收集到的是整个被成像区域内的质子发出的MR信号，这些信号不含有空间的信息。为了获得各个方向的空间信息，需要在Z轴、Y轴、X轴每个方向都施加一个梯度，分别被称为：

  • 层面选择梯度
  • 相位编码梯度
  • 频率（读出）梯度

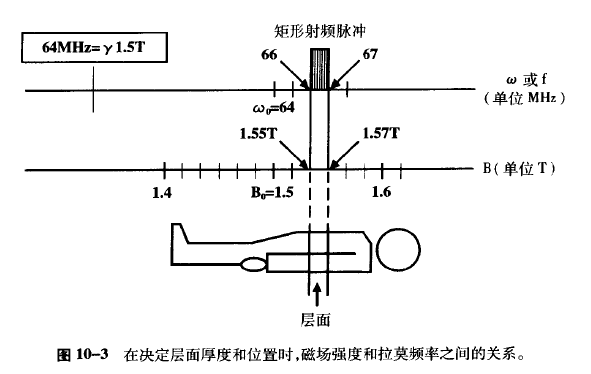
层面选择：在 z 方向上施加一个梯度变化的磁场 $G_z$，当我们向人体发射一个单一频率的射频脉冲，我们会获得一个以该频率进动的信号。但它是一个无限薄的平面，现实的做法是发射具有一定频率带宽的射频脉冲，获得一个有一定厚度的层面的信号。

降低层面厚度，可以通过：

  1. 减小射频脉冲的带宽
  2. 增大层面选择梯度

20250419171436

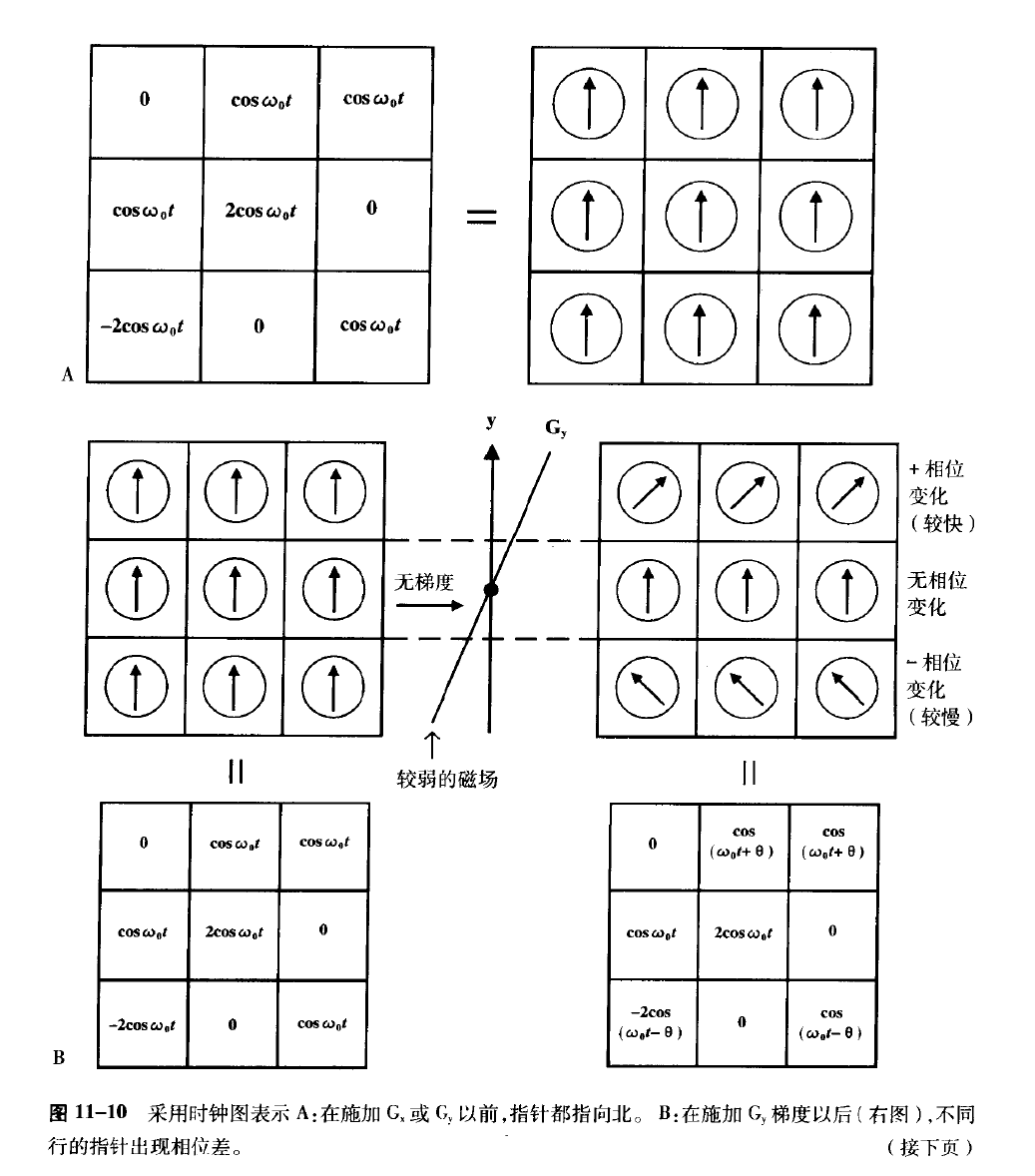
相位编码：层面选择只能让我们获得一整个层面的信息，为了获得每个位置的信号，在 y 方向上施加一个梯度 $G_y$， 此前以相同相位的质子出现了相位差，关闭 $G_y$ 后，质子以相同频率进动，但相位不同。

20250415234129

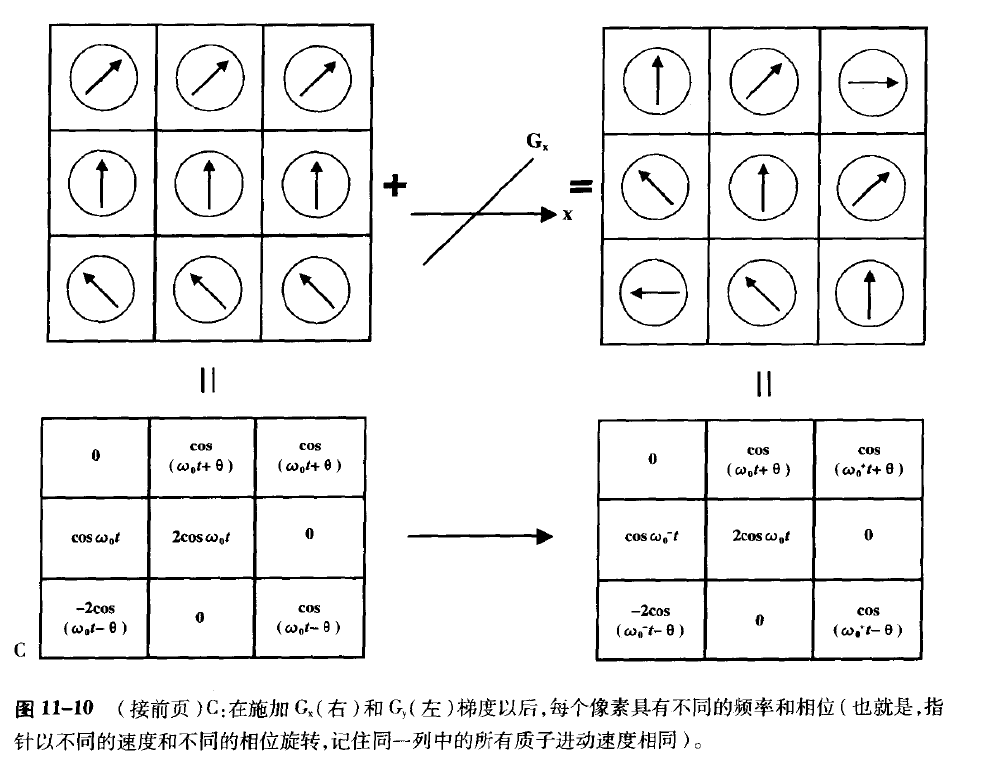
频率编码：打开 $G_x$ 后，频率也发生了变化，每个位置的信息都可以被计算出来。

20250415234232

接下来，如何得到每个位置的信号呢？

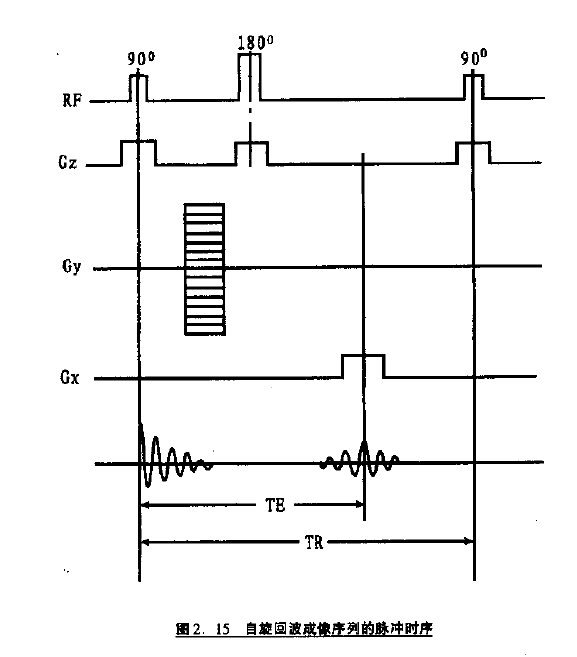
考虑一个基础的自旋回波脉冲序列， 首先是90°射频脉冲产生 FID 信号，同时打开 $G_z$ 进行选层，此时的这一层的质子产生的信号都是相同的，叠加在一起无法区分位置。接下来在 90° 和 180° 脉冲之间施加 $G_y$ 进行相位编码，然后在 TE/2 的时间施加 180° 脉冲使这个层面产生 SE 信号（$G_z$ 也是打开的），在接收回波期间打开 $G_x$，实现频率编码，并读出信号，此时的信号是由不同位置上不同相位和频率的所有质子产生的信号和，包含了所选层面上每个位置的信息。

20250419230037

为了区分每一行的像素，需要分别对每一行进行编码，每次的相位编码梯度以某个增量为基础成倍增加，在每个重复周期内， $G_Y$ 和 $G_x$ 各自持续时间内保持稳定的幅度。

一个相位编码梯度 = 一条K空间线 = 一个MRI信号 = 一个回波

如果需要 256 x 256 像素的图像，就需要相位编码重复 256 次，在每次接受到的信号上采样 256 个采样点，由此填充一个 256 x 256 的矩阵，也就是 K 空间矩阵。

每个层面都有自己的 K 空间。

20250420003322

K空间重建

K 空间的中心：

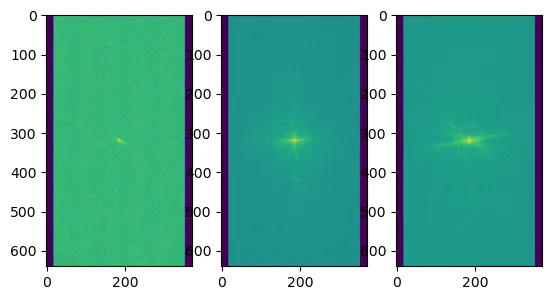
K空间的中心包含最大的信号，因为中间列具有最大的振幅，中间行没有失相位。由于信号本身的震荡， K空间图像中心区域信号较强，向外围逐渐减弱。

K 空间的对称性：

K空间在相位编码和频率编码方向分别对称（MRI快速成像的基石）。在实际应用中，梯度场的非线性和磁场的不均匀性可能会导致K空间数据的不对称性。

K空间中心部分具有更高对比度和信噪比，对于MRI重建非常重要，这也是多种序列必须优先甚至反复填充K空间中心的原因。

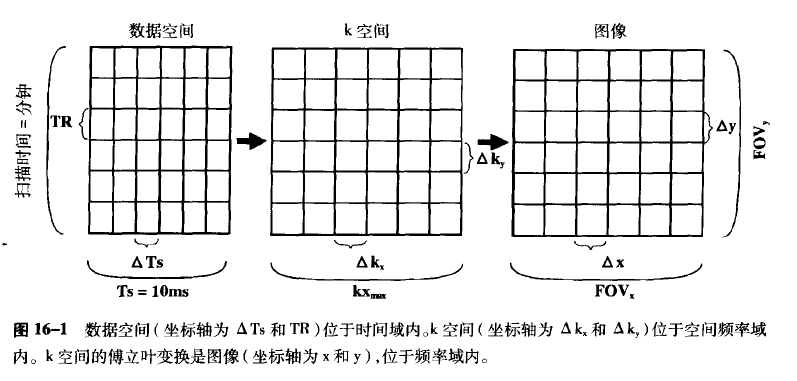
数据空间、K空间与图像：

20250422235732

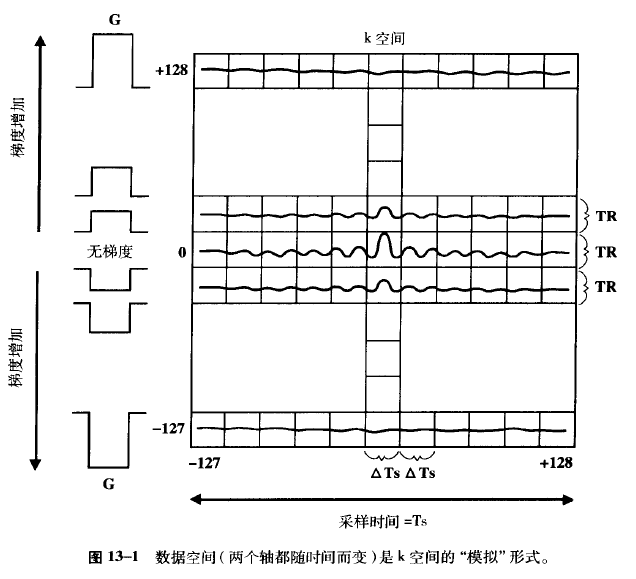
我们称最原始的采集到的数据为数据空间，在频率编码方向上，两次采样的时间间隔是微秒级，而在相位编码方向上采样间隔是秒级，这样的数据空间是一个与时间相关的频率信号，坐标轴单位是时间。

数据空间经过采样得到 K 空间数据，K 空间数据间隔与磁旋比、采样间隔和梯度强度有关，单位为 $周期/距离$。每一层的K空间里，在 x 方向上，存在着频率与位置的关系；在 y 方向上，存在着相位与位置的关系。这是一个与空间相关的频率信号。

对 K 空间进行傅里叶逆变换，可以将这个空间频率域信号（坐标轴单位：周期/距离）转为空间信号（坐标轴单位：距离）。

需要注意的是，K空间数据是频域信号，包括振幅和频率，每个K空间点都是是一个复数，包含实部和虚部，分别对应于信号的振幅和相位信息。

20250424223908

快速成像和图像重建

FSE/TSE

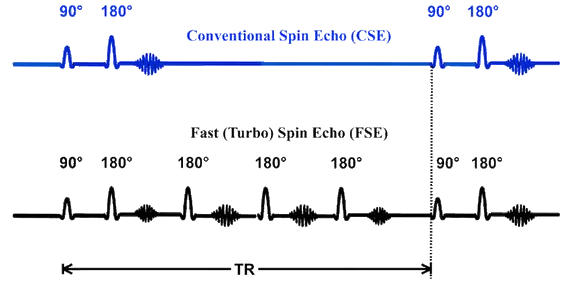
快速自旋回波 (Fast spin echo ，FSE) 成像，也称为涡轮自旋回波 (Turbo spin echo ， TSE) 成像。

传统的多回波序列以相同的相位编码收集一列回波，FSE/TSE 技术改变了每个回波的相位编码梯度。 由于在回波之间改变了相位编码梯度，因此可以在给定的重复时间（TR）内获取多行 k 空间（即相位编码步骤）。

20250424225253

由于在每个 TR 间隔内采集多条相位编码线，FSE/TSE 技术可大大缩短成像时间。 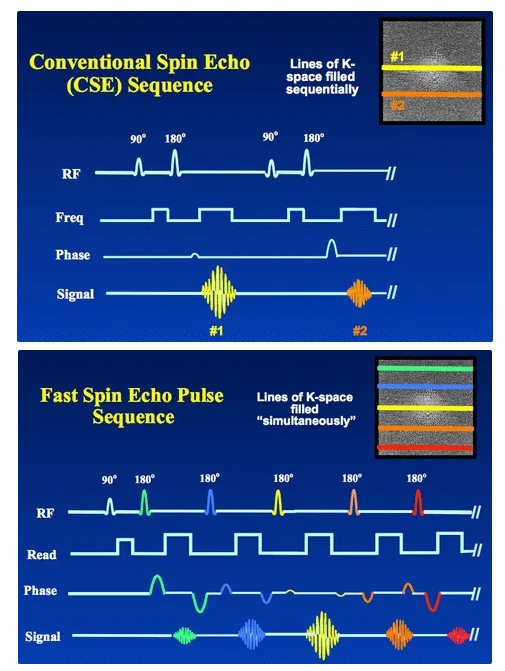20250424225546

在给定 TR 间隔内获取的回波数量称为回波序列长度 (ETL) 或 Turbo 因子。对于常规成像，ETL 的范围通常为 4 到 32，但对于快速成像/回波平面技术可能会超过 200。

当切片数量不是限制因素时，成像时间与 ETL 成反比。  也就是说，具有相同TR的传统SE序列的时间可以八分之一的时间来执行具有 ETL=8 的FSE/TSE序列。

参数

在传统的自旋回波（CSE）成像中，只需要指定两个基本定时参数：重复时间（TR）和回波时间（TE）。

TR和TE是基本脉冲序列参数，分别代表重复时间和回波时间。它们通常以毫秒 (ms) 为单位进行测量。 回波时间 (TE) 表示从射频脉冲中心到回波中心的时间。对于每个 RF 脉冲之间具有多个回波的脉冲序列，可以定义多个回波时间，通常标记为 TE1、TE2、TE3 等。 重复时间 (TR) 是重复的脉冲和回波系列上相应连续点之间的时间长度。

在快速/涡轮自旋回波 (FSE/TSE) 成像中， TE 被有效回波时间 (TEeff) 所取代，即 k 空间中心线被填充的时间。  此外，还需要两个新参数：

  • 回波数——GE和Canon称为 echo train length（ETL）；西门子和飞利浦的turbo factor ；或日立的shot factor。 回波序列长度 (ETL) 是最重要的参数。一般来说，图像采集时间与 ETL 成反比。  换句话说，如果具有一定TR/TE/空间分辨率的CSE序列需要8分钟来执行，那么ETL=8的FSE序列将只需要1分钟。 ETL 对图像质量也有重要影响。较长的 ETL 会导致更多的 T2 加权，因为更多的后期回波和较长的 TE 对整体信号有贡献。 较长的 ETL 还与整体信噪比 (SNR) 和对比度噪声比 (CNR) 的降低相关，因为后面的回波较弱。

  • 回波之间的时间——GE、Philips、Siemens 和 Canon 称为echo spacing (ESP)；日立公司的interecho time (ITE)。 增加回波间隔 (ESP) 允许使用更长的 TE，但会对 SNR 和 CNR 产生不利影响。  运动、敏感性和边缘相关伪影增加。  一般来说，增加 ESP 对图像质量有主要的有害影响；因此，在大多数应用中应选择允许的最短 ESP。

并行成像

磁共振成像的主要挑战之一是采集时间。对成像时间的主要贡献是相位编码步骤（PE）的数量，因为 TIME= NPETR/ETL 。

减少相位编码步数有几种传统方法，一种巧妙的方法是利用并行成像。这种技术的相控阵线圈的使用，相控阵线圈由覆盖整个容积的表面线圈阵列组成。使用表面线圈的好处是，它们对更小的空间敏感，噪声更少。然而，相控阵线圈的采用也激发了平行成像技术的发展。

体积线圈和相控线圈的区别是，体积线圈从整个封闭的体积接收信号，而相控阵中的独立线圈在每个位置的信号量都不同。

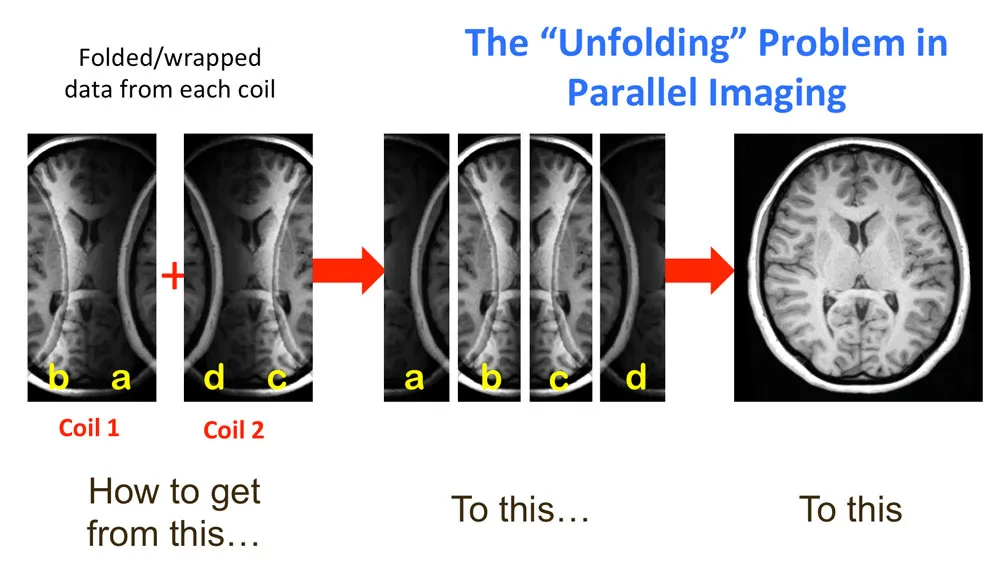
并行成像的原理是结合相控阵中单个线圈（或线圈组）提供的空间定位，”解除 “因视野缩小而产生的混叠。

20250424233539

因此，通过一点数学计算，我们可以重建全视场，而无需实际获取那些额外的相位编码步骤。减少的相位编码步数与全套步数之比称为加速因子 acceleration factor 或 R，它代表了节省时间的因子（以及缩小的视场大小）。

加速因子为2的并行采集图像在 K 空间中表现为隔行填充，相应的图像具有 1/2 的视野。根据采样定理，采样频率应该是信号最高频率的2倍以上，FOV应该大于成像的对象大小，否则会产生混叠伪影。

进行平行成像的第一步是找出每个线圈（或线圈组）的空间灵敏度。通常的做法是获取人体部位的极低分辨率图像。将所有线圈的数据合并形成平均图像（有时称为平方和，因为这是一种计算方法）。将每个线圈的图像除以平均值，就得到了灵敏度曲线。

图像重建（imagere construction）： 从成像体素的MR信号求解出图像矩阵中对应像素数据的后处理

  • 代数法：求解代数方程
  • 解析法：反投影法和傅里叶变化法

部分傅里叶重建方法

利用K空间的共轭对称性， 采集50%以上数据，再利用各种算法对未采集的数据进行填补，从而缩短扫描时间。部分傅里叶重建算法包括：零填充、共轭对称、Homodyne等，目的是实现相位矫正。这是由于在MRI设备中，采样时的运动、共振频率偏移、硬件延迟、涡流、磁场非均匀性等原因会造成数据的非完全对称，共轭对称的数据会引入相位错误

并行重建

并行重建方法主要分为两类，一类是在图像域分离混叠的伪影, 主要代表SENSE(1999), PILS(2000); 一类是在K空间解混叠，然后反变换回图像域，主要代表SAMSH(1997),AUTO-SMASH(1998), GRAPPA(2002)。SPIRiT 和 ESPRIT也是常见算法。

SENSE重建

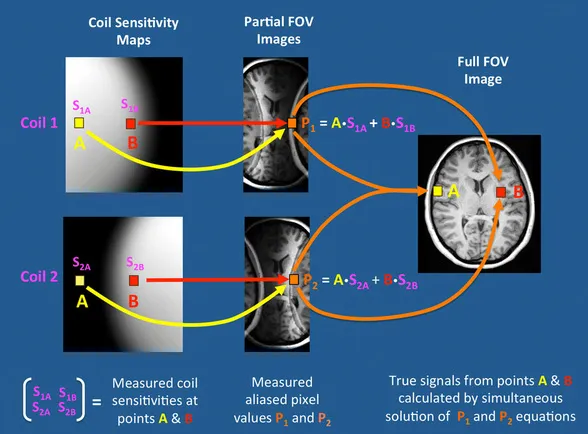
使用每个线圈的空间（不是 k 空间）灵敏度来展开锯齿图像。SENSE 利用了这样一个事实， 我们知道每个线圈在每个点上的相对信号强度，也知道真实空间中每个点在混叠图像上的映射位置，我们已经找到了每个线圈的灵敏度。我们还刚刚获取了混叠图像，分别记录了每个线圈的信号。然后，我们可以求解一些简单的方程。假设 P 是混叠图像中的点。这个点实际上代表了真实空间中叠加的两个体素，即 A 和 B。最后，我们将两个线圈的灵敏度分别称为 $S_1$ 和 $S_2$，两个线圈采集到的混叠图像在 P 处的值为 $P_1$ $P_2$，通过求解下面的方程可以得到 A B 处的值：

\[P_1 = S_{1A} * A + S_{1B} * B\] \[P_2 = S_{2A} * A + S_{2B} * B\]

20250424235727

只要 R ≤ 线圈，这对于任意数量的线圈和加速因子都适用。 平行成像的代价是信噪比降低。就像传统的缩小FOV（以及其他缩短采集时间的技术）一样，对身体部位采样的时间越少，信号就越差。等式与传统的缩小视野技术基本相同，但多了一个与线圈几何形状有关的系数 g： $SNR = SNR_{initial} / (g * √R)$

GRAPPA重建

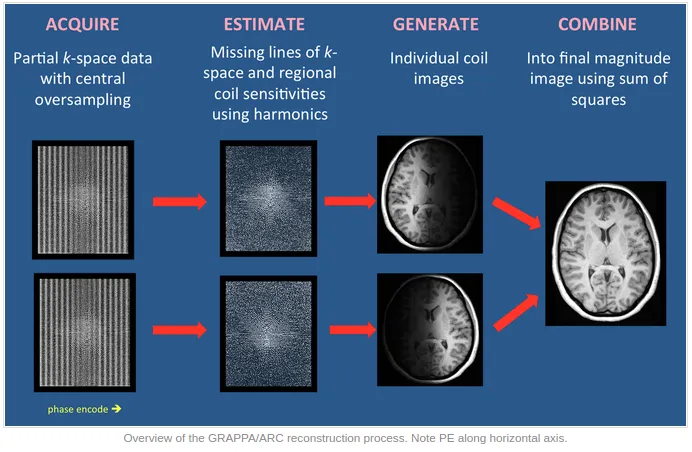
GRAPPA（通用自动校准部分并行采集）和 ARC（笛卡尔成像自动校准重建）是多线圈并行成像 (PI) 技术。与其他 PI 方法（例如 SENSE/ASSET）一样，GRAPPA/ARC 仅对有限数量的相位编码步骤进行采样。相位欠采样极大地减少了成像时间，但会导致必须解开的重叠/混叠信号。   在 SENSE/ASSET 中，线圈灵敏度用于在傅立叶变换后在图像域中整理这些信号。在 GRAPPA/ARC 中，校正是在傅立叶变换之前在 k 空间中进行的。SENSE/ASSET 方法重建，然后校正。GRAPPA/ARC 方法校正，然后重建。

20250425000342

GRAPPA/ARC 的关键步骤是估计缺失点。可以有很多变化，包括重建核的大小和使用的参数数量。GRAPPA 和 ARC 的主要区别在于，后者使用三维核来合成缺失数据，同时考虑到来自所有三个方向的相邻源数据。ARC 还采用了一种略有不同的估算过程，以使三维数据计算变得易于管理。

SMASH重建  Simultaneous Acquisition of Spatial Harmonics

该概念与 SENSE 完全相同，但数学重建是在 k 空间图像（和 k 空间线圈灵敏度）上完成的，而不是在真实空间中完成的。

线圈灵敏度的另一个问题是它们在很大程度上取决于患者（或身体部位）在扫描仪中的位置。在传统的 SENSE 和 SMASH 方法中，线圈灵敏度是在全分辨率扫描之前通过快速、低分辨率扫描获取的。如果患者在两次扫描之间移动或呼吸，则可能会完全扰乱重建。解决此问题的一种方法是以某种方式同时获取低分辨率、全视场扫描和高分辨率、缩小视场（锯齿）扫描。这实际上可以通过在加速扫描期间对 k 空间中心进行过采样来完成。换句话说，一次扫描将获取正常间距中 k 空间的中心线，但以 R 间隔的外围线。中心线用于设置线圈灵敏度，然后以正常方式重建全视场图像。这些技术称为 mSENSE（空间重建）和 GRAPPA（k 空间重建）。

其他重建方法：

  • SPIPiT重建
  • 同时多层重建方法
  • 三维并行成像

压缩感知重建

奈奎斯特-香农采样定理提供了指导：如果真实信号的最高频率低于采样率的一半，则可以使用正弦插值实现完美重建。压缩感知建立在这样一种理念之上：有了关于信号约束条件的先验知识，我们就可以使用更少的样本来重建信号。 CS 以低于采样定理的频率欠采样，通过非线性重建算法消除图像中的相干伪影，恢复欠采样K空间数据，得到重建图像。

基于深度学习的重建方法

… （太长了单开一篇写）

重建的评价指标

  • SSIM
  • PSNR
  • NMSE

参考：

  1. https://mriquestions.com
  2. MRI: The Basics
  3. 磁共振成像原理
  4. 【【老奇】核磁共振为何知道】 https://www.bilibili.com/video/BV1di4y1y7au/?share_source=copy_web&vd_source=4e494de71ad1c16a10ba764249055d5e
  5. http://xrayphysics.com/parallel.html
医学相关, 医学图像
MRI 医学图像 深度学习
本文由作者按照 CC BY 4.0 进行授权