MRI 成像(三): 基于深度学习的K空间加速重建方法
磁共振数据是在空间频域(称为 k 空间)中采集的,在k空间数据上应用傅里叶逆变换得到重建的空间图像。磁共振的采集速度受到相位方向编码上采集的 k 空间样本数量的影响,采集的K空间数据越少,速度越快。
根据香农-奈奎斯特采样定理,如果$\omega_{max}$ 是信号的最大频率,那么采样频率至少是最大信号频率的两倍,才能从采样信号中恢复出原始信号,也就是$\omega_{sampling}=\frac{1}{\Delta T_s} \geqslant 2\omega_{max}$。低于此最小值的采样会出现混叠,被称为欠采样。 对 k 空间中进行欠采样可以减少扫描时间,对欠采样 k 空间数据应用傅里叶逆变换会导致图像出现混叠伪影。
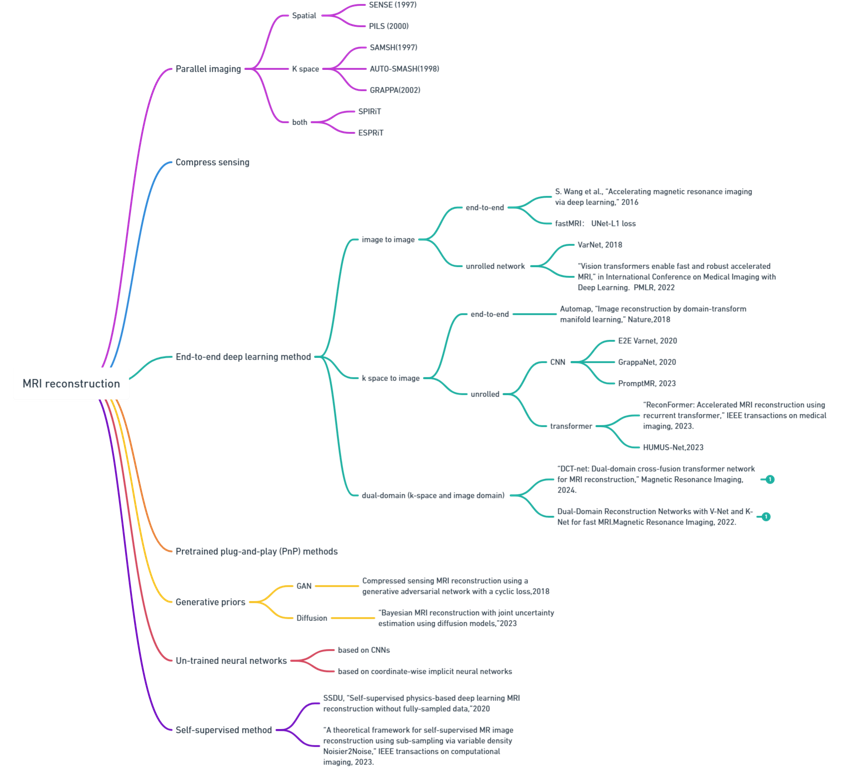
基于深度学习的MRI重建模型框架可以分为两类主要方法:物理驱动型和完全数据驱动型。虽然所有基于深度学习的方法都依赖于数据进行训练,但通过将MRI成像的物理过程(如傅里叶变换、数据一致性等)嵌入到深度学习模型中,确保重建过程符合物理规律,提高重建图像的质量和可靠性。而完全数据驱动型模型则仅依赖数据来学习重建,通过大量的训练数据学习输入(欠采样K空间数据)和输出(重建图像)之间的映射关系。
端到端模型
端到端的模型学习从欠采样数据到图像的映射,这种方法旨在通过网络直接生成重建图像,无需多次迭代,使其成为一种端到端解决方案,无需与特定数据采集方法紧密耦合。端到端方法可直接采用与图到图转换相同的模型,如 U-Net 、Swin Transformer 和生成对抗网络(GANs)、diffusion等。但与展开模型相比,端到端模型需要更大的数据集。
物理驱动模型
压缩感知(CS)使用稀疏先验进行重建,可以在欠采样的情况下恢复出原始信号。需要注意的是,压缩感知的重建过程通常需要解决一个非凸优化问题,即在满足欠采样数据的约束条件下,找到最稀疏的信号解。这通常需要使用迭代算法,并且对信号的稀疏性有较高的要求。
磁共振图像的重建过程可以看作是一个欠定线性逆问题,使用经典感知压缩算法解决优化问题,即找到满足下面公式的重建图像x,
\[A(x)+ ϵ= \hat{k}\],其中 $\hat{k}$ 是给定的欠采样 K 空间数据,其中缺失的数据用零填充。线性前向采样算子 $A()$ 包括了与线圈灵敏度图 $S$ 的逐点乘法、傅立叶变换 $F$ 和使用二进制掩码 $M$ 进行的欠采样操作, 即 $A(x)=MF(Sx)$。$ϵ$是采集噪声。
由于这个公式是欠定的,我们无法明确求解。因此,通常利用最小化最小二乘误差来求解: \(x = arg min_x ‖A(x)-\hat{k}‖_2^2 +λR(x)\) ,其中 $‖A(x)-\hat{k} ‖_2^2$ 是数据一致性项,保证重建数据与欠采样的数据相似,$R(x)$是 $x$ 上的稀疏正则化项,用以保证重建图像的唯一性,$λ$是用于控制权重的超参数。
最小二乘法的原理是对上述公式进行梯度下降,从而产生迭代算法,在迭代的第 $t$ 步,图像的通过下述公式更新: \(x^{t+1}=x^t-η^t(A^{*}(A(x)-\tilde{k} )+λR(x^t))\) 其中,$η^t$ 是学习率,$R$ 是正则化项的梯度,$A^*$ 是 $A$ 的自伴随矩阵。
基于压缩感知的重建需要复杂的非线性优化算法来重建图像,计算复杂度较高,特别是在大规模处理图像数据时,需可能需要大量的计算资源和时间,限制了感知压缩的应用。此外,超参数的选择对于图像重建的结果影响显著,需要手动选择。
传统的感知压缩技术对采集的速度提升有限,加速因子最大通常只能到4 或 5,之后图像质量就会严重下降。深度学习技术则有明显改善。与传统方法相比,深度学习模型能够实现更高的加速因子,提供更快的成像。
展开优化(unroll optimization) 通过将优化过程中的每个迭代步骤映射为一个神经网络模块,可以将传统的优化算法转化为一个可训练的神经网络结构。深度学习模型可以通过学习大量的图像数据得到关于图像的特征,例如稀疏性,从而作为正则化项来指导图像重建。VarNet 提出使用一个小的卷积神经网络作为正则化项, \(x^{t+1} = x^t-η^t(A^*(A(x)-\tilde{k})+ CNN(x^t))\)
这可以看作是一项图像到图像的任务,不包含k空间的信息,重建图像的质量有限。
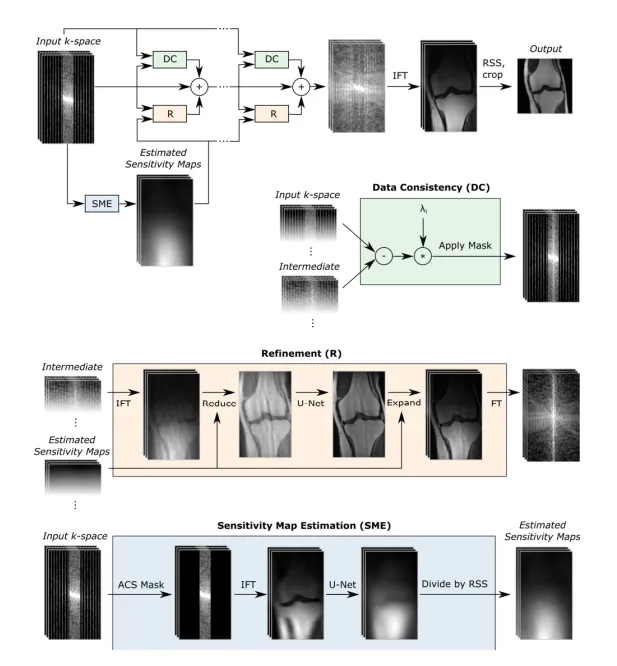
Sriram 等人提出的E2E-VarNet把上面公式中的图像换成了k空间数据,在k空间应用梯度下降来求解,并且使用了UNet模型作为正则化项: \(k^{t+1} = k^t-η^tM(k^t-\hat{k})+ Unet(k^t)\)
展开优化的方法在重建图像上效果较好,可以学习到更复杂的正则化项。然而这种方法需要多个模型的级联迭代,可能增加训练和推理的计算开销和时间。
Aggarwal 等人提出了 MoDL,采用基于 CNN 正则化的图像重建方法,其中包含针对复杂模型和图像先验的数值优化模块。基于变分模型且权重共享的公式化方法在数据约束条件下取得了更好的结果。
参考文献:
- Emerging Trends in Fast MRI Using Deep-Learning Reconstruction on Undersampled k-Space Data: A Systematic Review
- Advancing MRI Reconstruction: A Systematic Review of Deep Learning and Compressed Sensing Integration
- End-to-End Variational Networks for Accelerated MRI Reconstruction
- HUMUS-NET: hybrid unrolled multi-scale network architecture for accelerated MRI reconstruction